The domain and range of the function f(x) = x 2 has to be determined The domain of a function is all values of x for which the value of f(x) is definedFirst week only $499!1 find the domain and range of f(x) 2 cos3x close Start your trial now!

Find The Domain And Range And Describe The Level Chegg Com
How do you find domain and range of a function
How do you find domain and range of a function-Mathx\text{,}\text{ }y\in\R\text{}/math Let mathy=f(x)\textThe domain and range are the intervals in which the function is defined in the x and y axes Answer and Explanation 1 We are given the function {eq}f(x)=2x^23x1 {/eq}
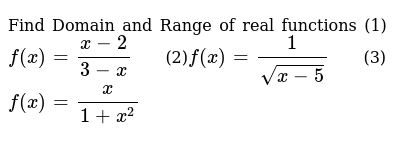



Find Domain And Range Of Real Functions 1 F X X 2 3 X 2 F X 1 Sqrt X 5 3 F X X 1 X 2
3 answers 218 people helped given function is f (x)=x2−9x−3 since the denominator can not be zero x−3≠0⇒x≠3 the domain of the function is R− {3} y=f (x)=x2−9x−3y= (x−3) (x3)x−3y=x3 for x∈R− {3}y≠33 f (x) is not defined for x=3y≠6 range of the function is R− {6} hope this helps youThe domain is all real numbers, and the range is all real numbers f(x) such that f(x) ≤ 4 You can check that the vertex is indeed at (1, 4) Since a quadratic function has two mirror image halves, the line of reflection has to be in the middle of two points with the same y value Therefore, the range of f(x) is the union of the range of the two pieces, namely y > 1 (When x = 15, y = 1, so y = 1 is clearly in the range of f(x)) I ended up making a table of values in a spreadsheet to determine the range It seems that the fact that the function is fractional with an absolute value is throwing us off
f = { ("x , " 𝑥2/(1𝑥2)) x ∈ R } We find different values of 𝑥2/(1 𝑥2) for different values of x Domain Value will always be between 0 & 1 We note that Value of range y = 𝑥2/(1 𝑥2) is always positive Also, it is always between 0 and 1 Hence, Range is any positive integer between 0 and 1 with 0 included Thus, Range of f = 0, 1) Mathematics High School verified answered • expert verified For the function f (x) = 3 (x − 1)2 2, identify the vertex, domain, and range The vertex is (1, 2), the domain is all real numbers, and the range is y ≥ 2 The vertex is (1, 2), the domain is all real numbers, and the range is y ≤ 2Find the domain and range of the following functions f(x) = 1 x 2 Solution For any values values of x, the function will give defined values It will never become undefined So, domain is all real values that is R The range of x 2 lies between 0 to ∞ But we need find the range of 1 x 2 0 ≤ x 2 ≤ ∞ Multiplying by negative through out the inequality, we get ∞ ≤ x 2 ≤ 0 Add 1
The domain and range of real function f defined by f(x) = √x 1 is given by askedin Sets, Relations and Functionsby Sima02(493kpoints) relations and functions class11 0votes 1answer Find the domain and range of the following real functions f(x) = √x^24Arithmetic Mean Geometric Mean Quadratic Mean Median Mode Order Minimum Maximum Probability MidRange Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution Physics f(x)=\frac{1}{x^2} domain\y=\frac{x}{x^26x8} domain\f(x)=\sqrt{x3} domain\f(x)=\cos(2x5) domain\f(xFirst week only $499!




How To Find The Domain And Range Of A Function 14 Steps
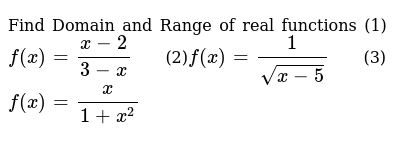



Find Domain And Range Of Real Functions 1 F X X 2 3 X 2 F X 1 Sqrt X 5 3 F X X 1 X 2
The first position can be filled with 1 or 2 or 3, therefore there are three different ways to fill the first one The second and the third position can be filled with three different ways, tooThe values taken by the function are collectively referred to as the range For example, the function x2 x 2 takes the reals (domain) to the nonnegative reals (range) The sine function takes the reals (domain) to the closed interval −1,1 − 1, 1 (range)Algebra Find the Domain and Range f (x)= (x^21)/ (x1) f (x) = x2 − 1 x − 1 f ( x) = x 2 1 x 1 Set the denominator in x2 −1 x−1 x 2 1 x 1 equal to 0 0 to find where the expression is undefined x−1 = 0 x 1 = 0 Add 1 1 to both sides of the equation x = 1 x = 1




4 Ways To Find The Range Of A Function Wikihow
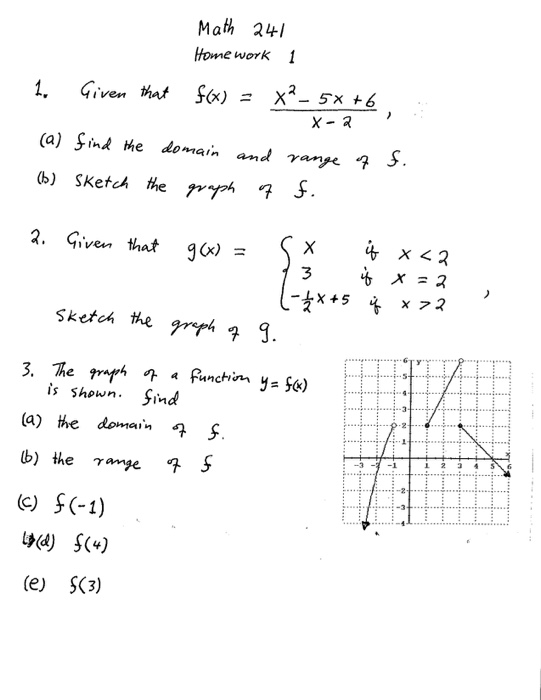



1 Given That F X X 2 5x 6 X 2 A Find The Domain Chegg Com
The range of f is given by the interval 0 , infinity) c To sketch the graph of f(x) = x 2, we first sketch the graph of y = x 2Arrow_forward Question View transcribed image text fullscreen Expand check_circle f (x)= x^2 5 The domain are all x values that has images As you see, we do not have any restrictions on the values of x ==> Therefore, the domain is all real numbers As for the range




Graph F 1 X Identify The Domain And Range Of Chegg Com



What Is The Range Of 1 X 2 1 Quora
Algebra Q&A Library 1 find the domain and range of f(x) = 2 cos3x 1 find the domain and range of f(x) = 2 cos3x close Start your trial now!See Answer Check out a sample Q&A here Want to see this answer and more?Functions assign outputs to inputs The domain of a function is the set of all possible inputs for the function For example, the domain of f (x)=x² is all real numbers, and the domain of g (x)=1/x is all real numbers except for x=0 We can also define special functions whose domains are more limited Google Classroom Facebook Twitter




Misc 4 Find Domain And Range Of F X Root X 1 Chapter 2




Domain And Range Of Quadratic Functions Video Khan Academy
X ≤ 4 or x≥ −4 Then, The domain−4,4 Range f (x) is maximum at x = 0,f (x) = 4 And f (x) is minimum at x= 4,f (x)= 0 Range 0,4 Hence, this is the answer Answer verified by Toppr ️Given real function is f(x) = x/1x^2 ️1 x^2 ≠ 0 ️x^2 ≠ 1 ️Domain x ∈ R ️Let f(x) = y ️y = x/1x^2 ️⇒ x = y(1 x^2) ️⇒ yx^2 – x y = 0 ️This is quadratic equation with real roots ️(1)^2 – 4(y)(y) ≥ 0 ️1 – 4y^2 ≥ 0 ️⇒ 4y^2 ≤ 1 ️⇒ y^2 ≤1/4What is the domain and range of the real function f(x)=1/(1x^2)?
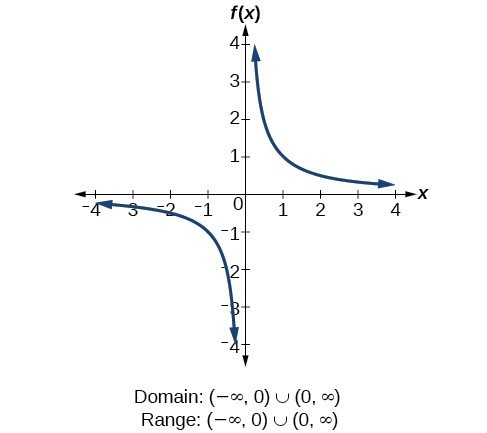



Determine Domain And Range From A Graph College Algebra




Given F X X 1c2x 8 G X 2x 8cx 1 And H X F X G X Then Which Of The Following Holds
Find Domain and Range of real functions (1) `f(x)=(x2)/(3x)` (2)`f(x)=1/sqrt(x5)` (3) `f(x)=x/(1x^2)`SOLUTION find the range and domain f (x)=1/x2 Question find the range and domain You can put this solution on YOUR website!This is a revised answer!




Find The Domain And Range Of The Function F X Sin 1 X 2 2




Find The Range Of Each Of The Following Functions F X X 3 F X 1 X 2 F X X 4 Youtube
The rule f(x) = x^2 is a bijection if the domain and the codomain are given by (a) R,R (b) R, (0, ∞) (c) (0, ∞), R Domain ( − ∞, ∞) Range ( − ∞, ∞) Square Root f(x) = 2√x, commonly just written as, f(x) = √x Domain 0, ∞) Range 0, ∞) When dealing with the set of real numbers we cannot take the square root of a negative number so the domain is limited to 0 or greater Absolute Value Function f(x) = xWhen the given function is of the form f(x) = 1/(x – 1), the domain will be the set of all real numbers except 1 In some cases, the interval be specified along with the function such as f(x) = 3x 4, 2 < x < 12 Here, x can take the values between 2 and 12 as input (ie domain)
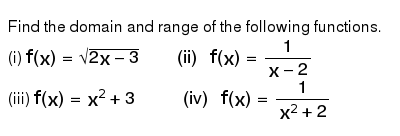



0 5 Find The Domain And Range Of The Following Function 2 F X




Find The Range Of I F X X 4 X 4 And Domain Of Ii F X 1 Log 10 1 X Sqrt X 2 Youtube
The domain is all real numbers, and the range is all real numbers f(x) such that latexf(x)\leq4/latex You can check that the vertex is indeed at (1, 4) Since a quadratic function has two mirror image halves, the line of reflection has toAll domain name registrations include 24hr phone support, free URLforwarding and free DNS hosting √X^2–1 is not equal to 0 , X^2–1 is not equal to 0 also, (X1) (X1) is not equal to 0 & X is not equal to 1 & 1 For root function to be defined X^2–1>=0 (1) (X1) (X1)>=0 (2) Range (f)= {YY€R}=R {0} Step 1 Draw the graph Step 2 Find the possible values of x where f (x) is defined Here the x values start from 2 and ends in 2 Step 3 The possible values of x is the domain of the function ∴ \therefore ∴ the domain of the circle is { x ϵ R − 2 ≤ x ≤ 2 x\epsilon \mathbb {R}2\leq x\leq 2 xϵR −2 ≤ x ≤ 2 } =



How Do We Draw The Graph And Find The Range And Domain Of The Function F X X 1 Quora




Function And Their Types Q5 Determine The Domain Chegg Com
The domain and range of the function f= ((1/1x2)) x ∈ R, x ≠ ± 1 are respectively Q The domain and range of the function $f=\left\{\left(\frac{1}{1x^{2}}\right) x \in R, xClick here👆to get an answer to your question ️ Find the domain and range of the function f (x) = x ^2/1 x ^2Write the Domain and Range of the Function F ( X ) = X − 2 2 − X CBSE CBSE (Science) Class 11 Textbook Solutions Important Solutions 9 Question Bank Solutions 9938 Concept Notes & Videos 580 Syllabus Advertisement Remove all ads Write the Domain and Range of the Function F ( X ) = X − 2 2 − X




Find The Domain And Range Of The Following Real Functions I F X X Ii F X Sqrt 1 X 2




Find The Domain And Range Of The Function Defined By F X 1 9 X Please Help Me Brainly In
Here we are given a real function Hence, both domain and range should be real numbers Here, x can be any real number Here, f(x) will always be positive or zero Here value of domain (x) can be any real number Hence, Domain = R (All real numbers) We note that that range f(x) is 0 or positive numbers, So range cannot be negative Hence, Range = Non negative realFind the domain and range for the function f(x)=(5 x2) /(2 x1) 💬 👋 We're always here Join to connect with other students 24/7, anytime, night or dayFree functions range calculator find functions range stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy
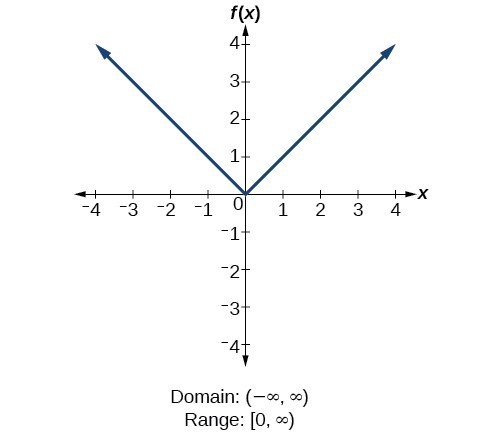



Find Domains And Ranges Of The Toolkit Functions Math 1314 College Algebra




Find Domain And Range Of Function Y 1 X Youtube
Set the denominator equal to zero Remember, dividing by 0 is undefined So if we find values of x that make the denominator zero, then we must exclude them from the domain Now to find the range, notice thatThe x intercepts is at the point (2 , 0) b The domain of f is the set of all real numbers Since x 2 is either positive or zero for x = 2; For log function domain is x values greater than 0 because log argument cannot be negative So, for the given function domain is x>0 Range is the set of f(x) values for which the function is defined In log function , for every value of x the f(x) values can be positive , negative or zero so range is all real numbers
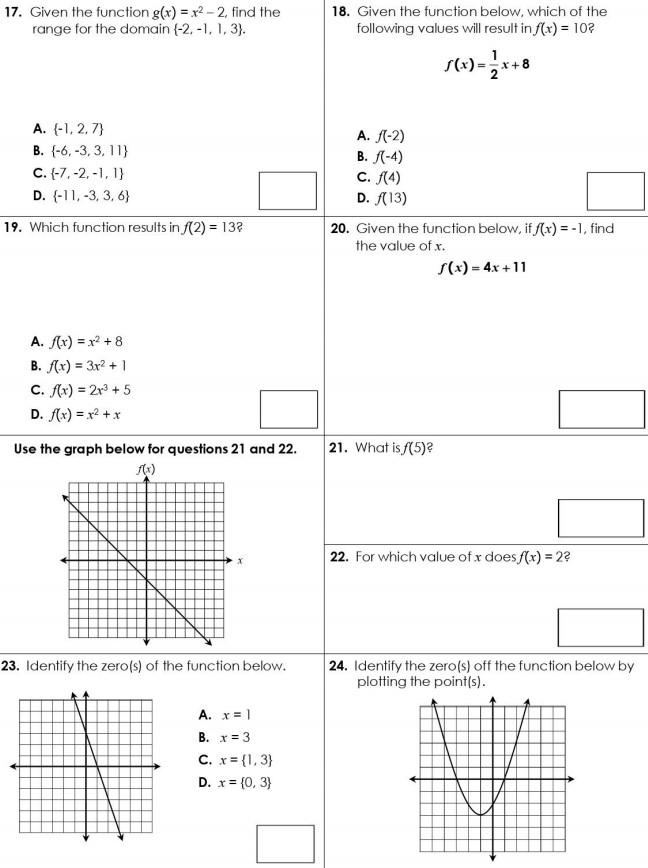



17 Given The Function G X X2 2 Find The Range Chegg Com



Domain And Range Examples Domain And Range Of Functions
Domain and range graph The graph of f(x)=x2 f ( x) = x 2 (red) has the same domain (input values) as the graph of f(x)=− 1 12x3 f ( x) = − 1 12 x 3 (blue) since all real numbers can be input values However, the range of the red graph is restricted to only f(x)≥0 f ( x) ≥ 0, or y y values above or equal to 0 0For f(x) = x 2, the domain in interval notation is D (∞, ∞) D indicates that you are talking about the domain, and (∞, ∞), read as negative infinity to positive infinity, is another way of saying that the domain is "all real numbers" The range of f(x) = x 2 in interval notation is R 0, ∞) R indicates that you are talking aboutAssuming "domain" is referring to a real function property Use as a plotting function instead




F X Log 1 3 H A Domain 0 Range B Domain 0 Homeworklib
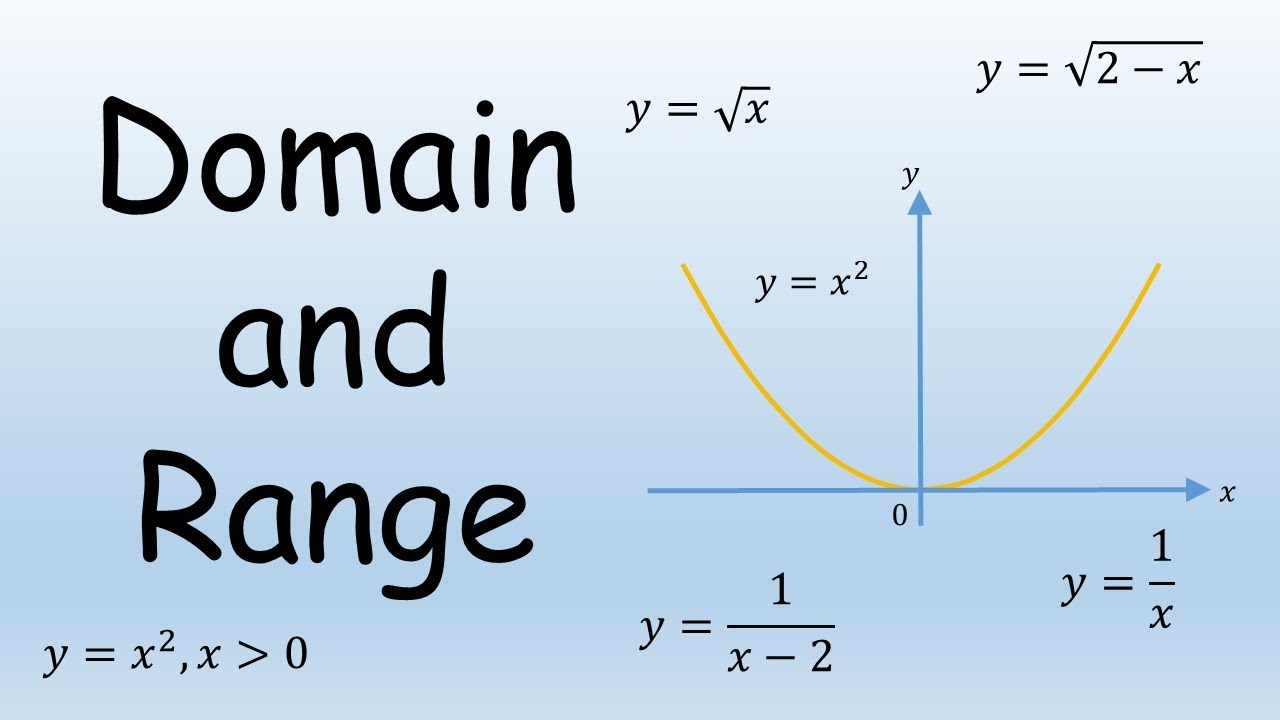



Find Domain And Range Of Function Y 1 X Youtube
Arrow_forward Question View transcribed image text fullscreen Expand check_circle Expert Answer Want to see the stepbystep answer?Answer and Explanation 1 Given f(x) = 1 x f ( x) = 1 x Domain Since the function is a fraction, the value of the variable are all real numbers except 0 0 since it will result to an undefinedFind the domain and range of the function $$f(x) = \sqrt{x^2 25} $$ and $$ f(x) = \sqrt{25 x^2}$$



Find The Domain And Range Of F X 2x 5 Mathskey Com
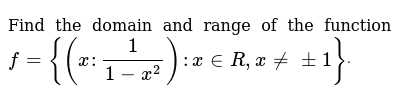



Find The Domain And Range Of The Function F X 1 1 X 2 X In R X 1 Dot
What is the domain and range of $$ f(x) = \frac{2e^x}{1e^x} $$ and the domain and range of $$ f^{1}(x)$$ I've already found $$ f^{1}(x) = \ln\left(\frac {x}{2x}\right) $$ I'm looking for the process necessary to find its domain and range Many thanksAlgebra Find the Domain and Range f (x)=x^21 f (x) = x2 1 f ( x) = x 2 1 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval Notation




Example 15 F X 1 X What Is The Domain And Range Examples




If F X X 2 X X 2 2x Then Find The Domain And Range Of F Show That F Is One One Youtube



Domain And Range Of Exponential And Logarithmic Functions




The Graph Models The Function F X 2 1 2 X What Is The Domain And Range Of The Function A Domain Brainly Com




Find The Domain And Range Of The Function F X 16 X 2 Donimain




Find Domain And Range Of F X 1 16 X 2 Brainly In




If F X X2 1gx X2 1 Find F G X Identify The Chegg Com




Find Domain And Range Of Real Functions 1 F X X 2 3 X 2 F X 1 Sqrt X 5 Youtube



Q Tbn And9gcrbtq2n2wyqxjku7shcld Gzp Crxxctbrkotgywsn Sp4ftbet Usqp Cau




4f 1 3 0 2 5 3 4ト 3 3 A Find The Domain Chegg Com



What Is The Domain And Range Of 1 X 3 Quora




Find The Domain And Range Of The Real Function Fx 1 1 X 2 Brainly In




Find The Domain And Range Of The Function F X 1 2 Sin3x Youtube




Misc 5 Find Domain And Range Of F X X 1 Class 11




The Problem Was To Graph The Function Find The Chegg Com
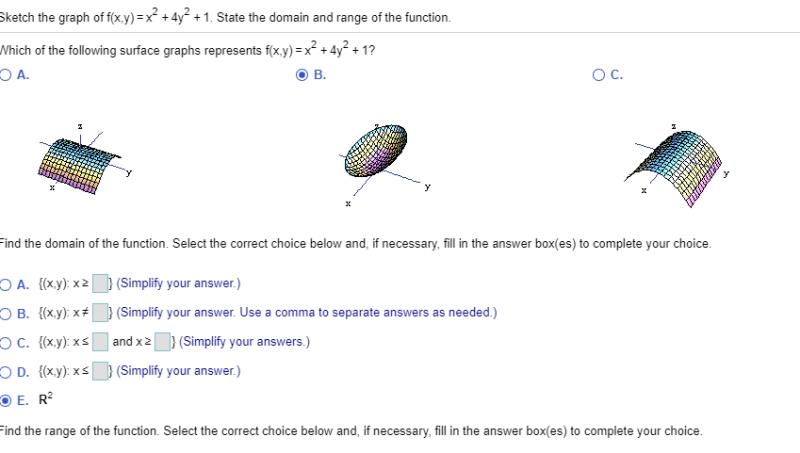



Sketch The Graph Of F X Y X 4y2 1 State The Chegg Com



Problem 9 Let F X 2 3x4 On The Largest Domain For Which The Formula Makes Sense A Find The Domain And Range Of F X Then Sketch The Graph Course Hero
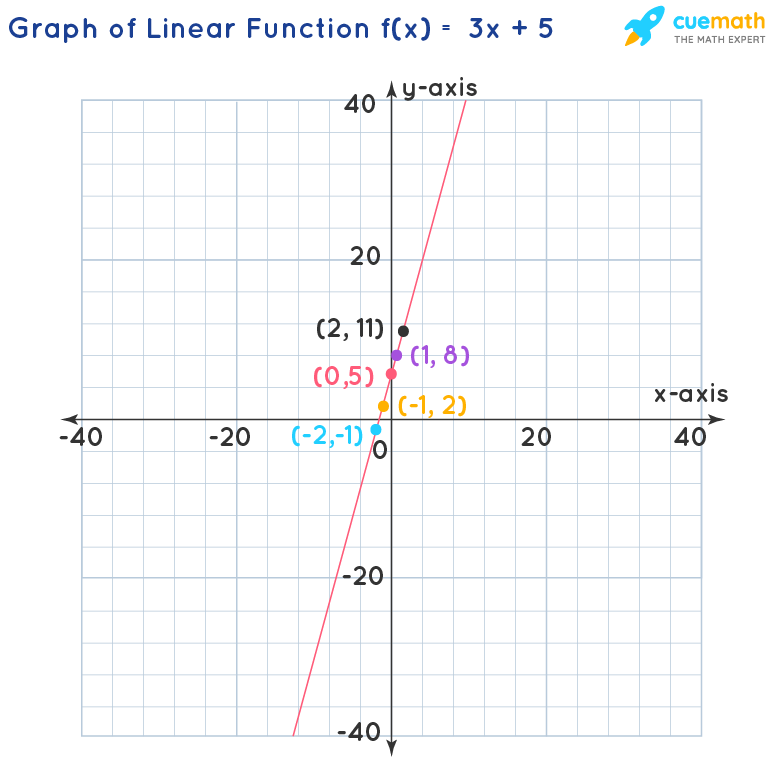



What Are The Domain And Range Of The Function F X 3 X 5 Solved



For The Function F X X 2 5 Find The Domain And Range Enotes Com
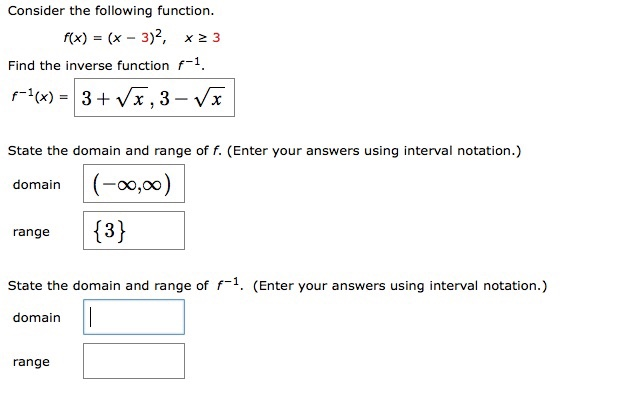



Consider The Following Function F X X 3 2 X 2 3 Chegg Com




View Question Domain And Range




Find The Domain And Range Of The Function F X 2 8 Chegg Com




Find The Domain And Range And Describe The Level Chegg Com




F X 2x 1 Find Domain And Range Brainly In



How Do You Find The Domain And Range Of T 1 3 Socratic




Find Domain And Range Of Function Let A 2 1 0 1 2 And F A Gtz Be Given By F X X 2 2x Youtube
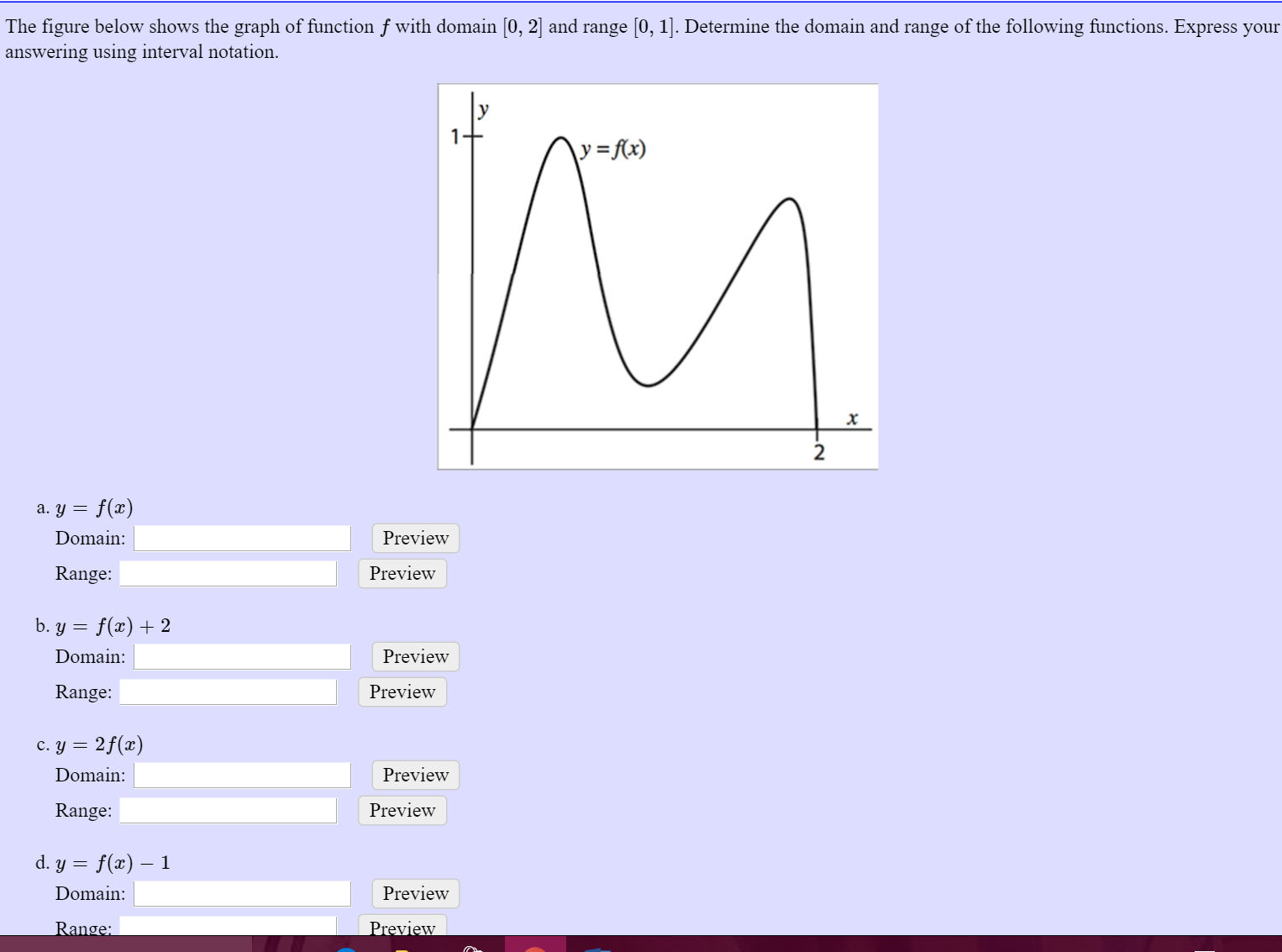



The Figure Below Shows The Graph Of Function F With Chegg Com
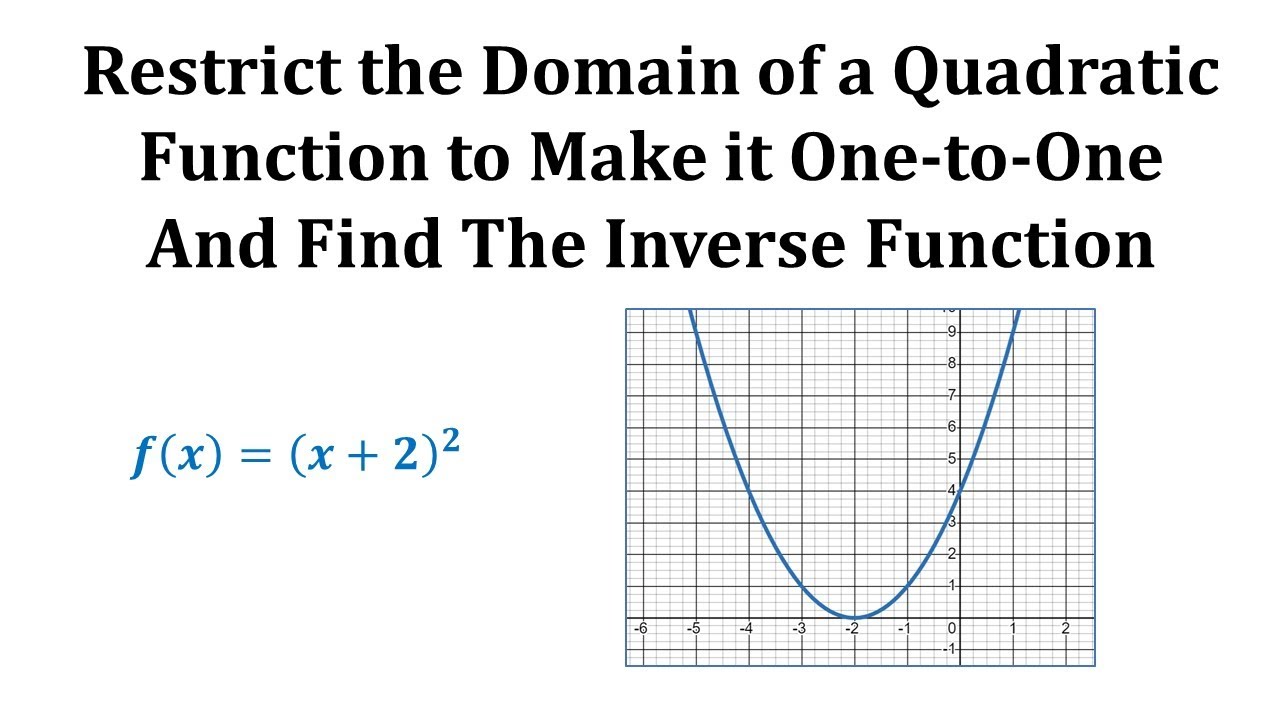



Ex Restrict The Domain To Make A Function 1 To 1 Then Find The Inverse Youtube
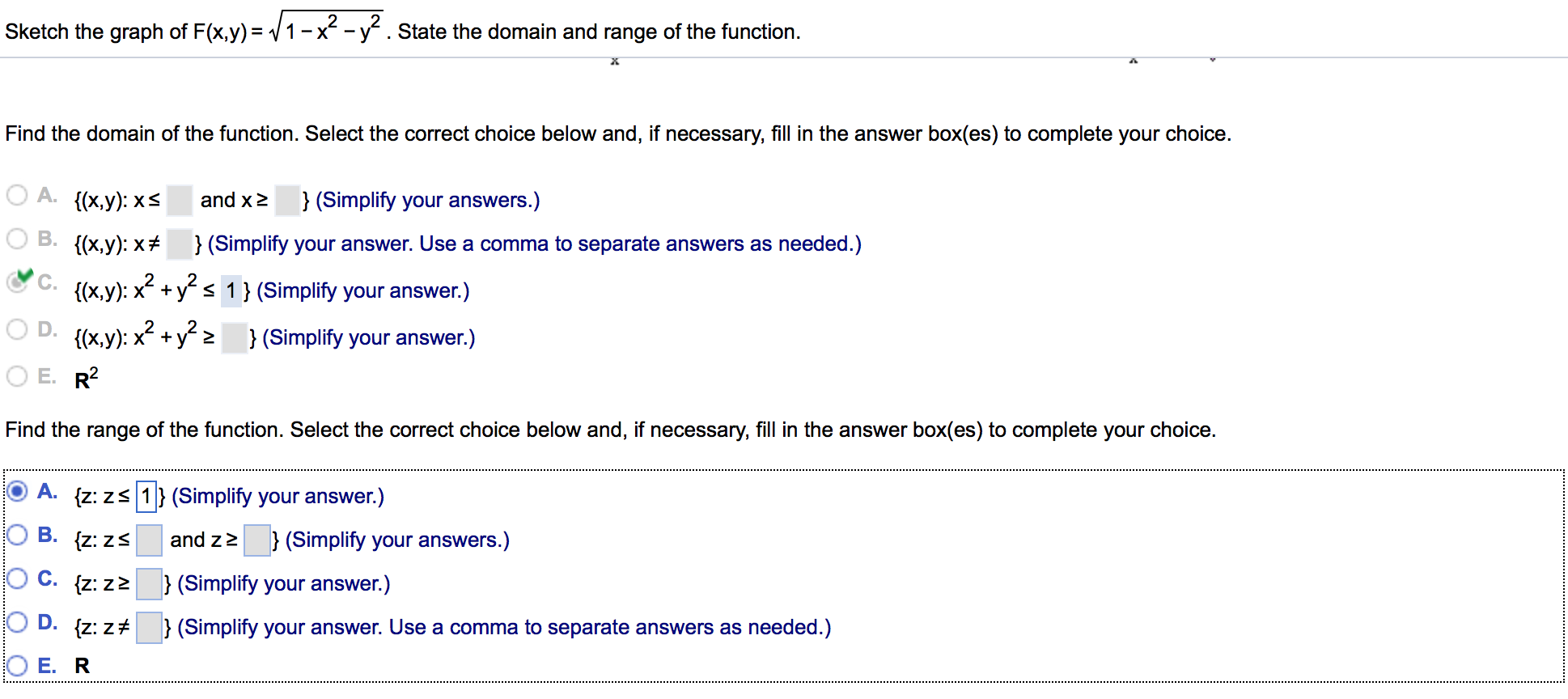



Sketch The Graph Of F X Y Squareroot 1 X 2 Chegg Com




Find The Domain And Range Of The Function F X 16 X 2 Donimain




2 Find The Vertex Domain Range X And Y Chegg Com




What Are The Domain And Range Of F X 1 6 X 2 Brainly Com




Find The Domain And Range Of The Function F X Y Chegg Com



Domain And Range Of Rational Functions




Find The Domain And Range Of The Functions G X Y Chegg Com




Find Domain And Range Of Function Y 2 X 2 X 2 4 Youtube



Q Tbn And9gcqgqrwpnxjwt0kskruy6guwbb9vrtxcyvozrczh7yys7zu6fw5a Usqp Cau




Find The Domain And Range Of The Function F R To R F X X 2 1




What Is The Domain And Range Of F X Abs X 3 5 2 Socratic




What Are The Domain And Range Of F X 1 5 X Brainly Com




If The Function F X X2 Has The Domain 0 1 4 9 Chegg Com



The Domain And Range Of The Function F X X 2 Is Donimain




Mtu 6 5 Points Each Find The Domain And Range For F X A F X 2 Homeworklib




Find The Domain And Range Of The Following Functions I F X X 2 Ii F X X 1 3 X



How Do You Find The Domain And Range Of Y Sqrt 3x 5 Socratic




Let F X Y Z 1 X 2 Y 2 Z 2 Find The Domain Chegg Com




Section 1 1 Relations And Functions Relation Domain Range Function Example 1 State The Domain And Range Of Each Relation Then State Whether Ppt Download




1 4 Pts State The Domain And Range Of F X 1 X Chegg Com



How To Find The Domain Of A Function



What Is The Domain And Range Of F X X 1 X 2 1 X 3 Quora



Domain And Range Of A Function




If The Function F X Has A Domain Of 2 X 8 And A Range Of 4 Y 6 And The Function G X Is Defined By The Formula G X 5f 2x Then What Are




Misc 6 Let F X X2 1 X2 X R Find Range Chapter 2
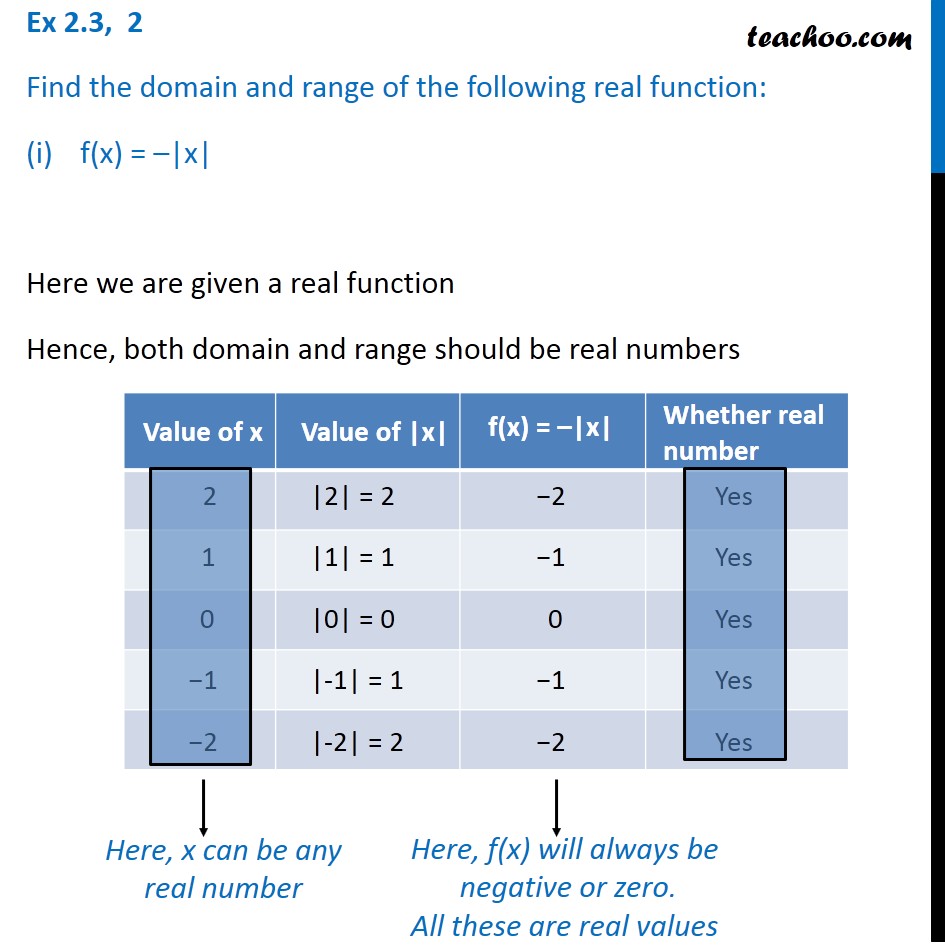



Ex 2 3 2 Find Domain And Range I F X X Chapter 2




Find The Domain And Range Of F X 7x 2 4x 1 Brainly In




Find The Domain And Range Of The Function F X 1 1 X 2 X In R X 1 Dot
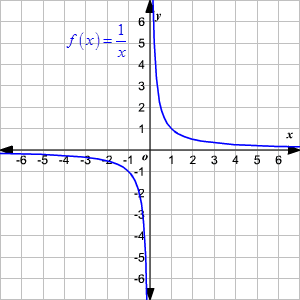



Domain And Range Of Rational Functions



What Is The Domain And Range Of X 2 1 X 2 Quora




L1 Functions Domain Amp Range
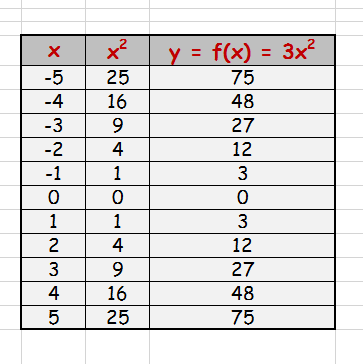



How Do You Find The Domain And Range Of Y 3x 2 Socratic



What Is The Domain And Range For The Following Function And Its Inverse F X 3x 1 2 Mathskey Com
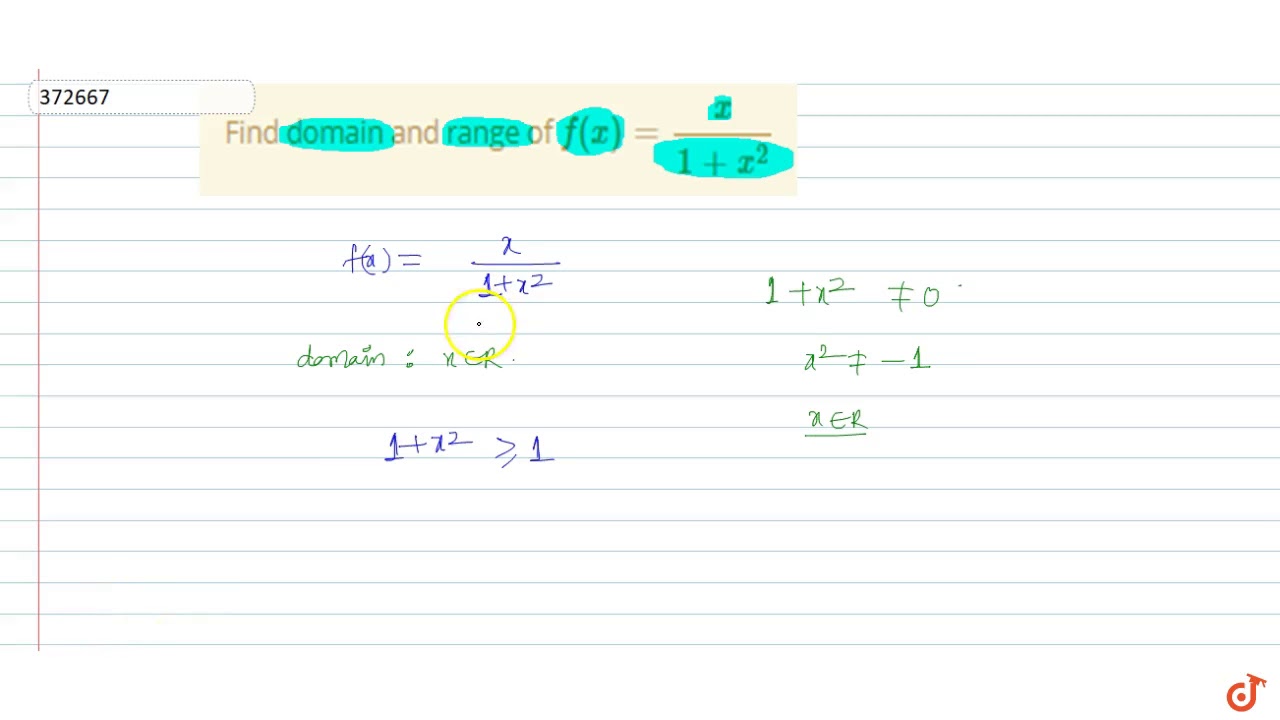



Find Domain And Range Of F X X 1 X 2 Youtube
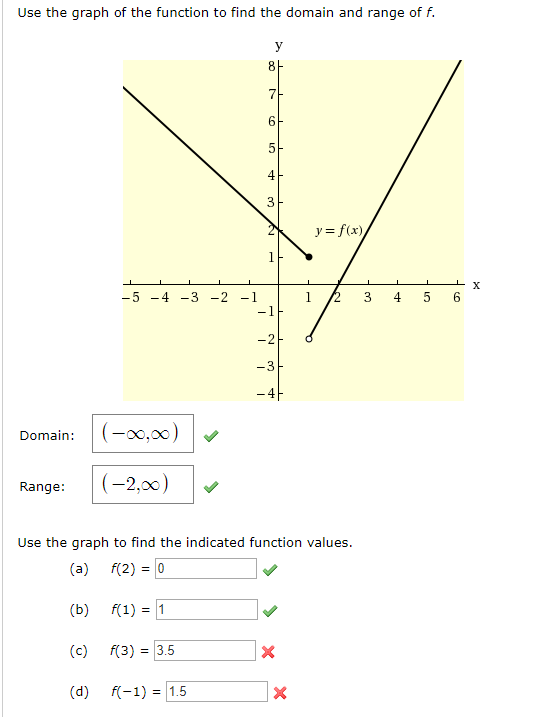



Use The Graph Of The Function To Find The Domain And Chegg Com
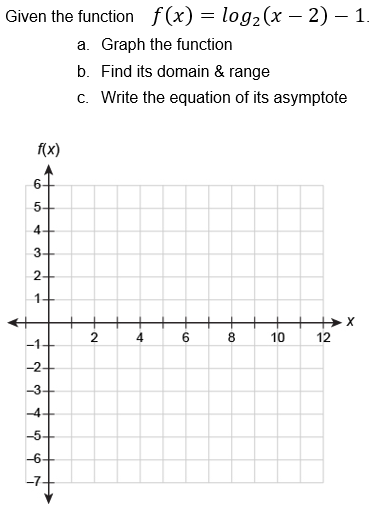



Given The Function F X Log2 X 2 1 A Graph Chegg Com




Domain And Range Calculator Wolfram Alpha




Look At The Function F X X 2 2 Which Of The Following Describes The Domain And Range Of The Brainly Com
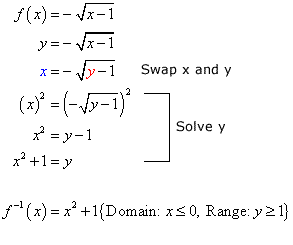



Inverse Of Square Root Function Chilimath



1



What Is The Domain And Range Of X 2 1 X 2 Quora




Domain And Range Of 1 X 2 2x 8 Youtube




Find Domain And Range Of Real Functions 1 F X X 2 3 X 2 F X 1 Sqrt X 5 3 F X X 1 X 2
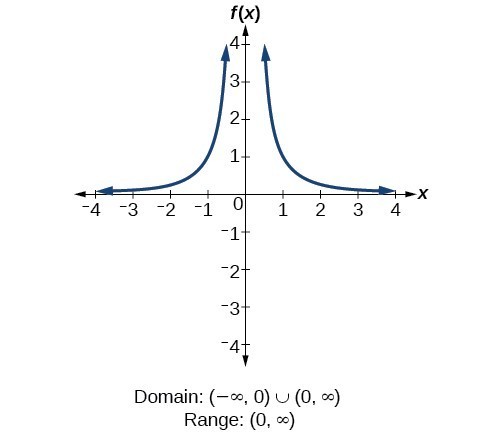



Determine Domain And Range From A Graph College Algebra




Consider The Function F X Y Ln X 2 Y 2 1 Chegg Com




Graph Each Function Give The Domain And Range See Chegg Com
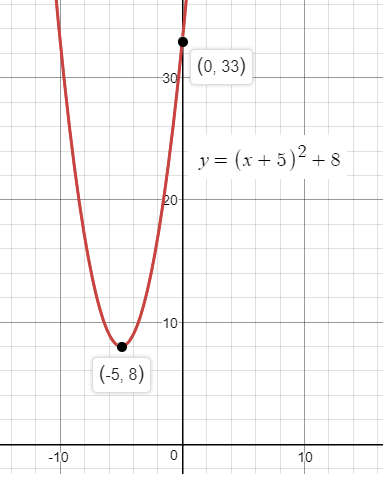



How Do You Find The Domain And Range Of F X X 5 2 8 Socratic



Draw The Graph Of The Function F X X 2 And Write Its Domain And Range Sarthaks Econnect Largest Online Education Community
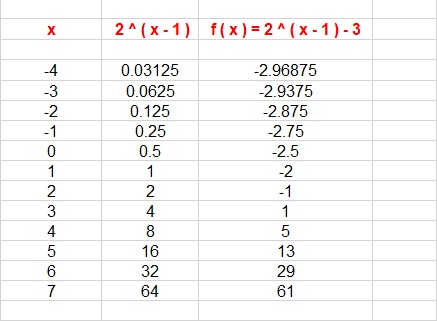



How Do You Graph F X 2 X 1 3 And State The Domain And Range Socratic




Find The Domain And Range Of The Function F X Chegg Com



0 件のコメント:
コメントを投稿